A couple of days ago, I read the book "Make Your Own Neural Network" from Tariq Rashid. It's an introduction to neural networks.
The book describes how to build a trivial feedforward neural network with forward propagation and backpropagation.
If you already know the basics of neural networks, you will not learn anything from this book. But for me, that knew nothing before reading the book. It was a good introduction.
The digital version of the book cost about 4 USD on Amazon.
In the first part of the book, the author covers the basics of neural networks and, in the second part, presents an example with the MNIST dataset.
The MNIST database is a large database of handwritten digits. It is widely used for training and testing machine learning algorithms.
The database consists of 60,000 training images. Each image has a size of 28 x 28 pixels and depicts a digit between 0 and 9. The collection also provides 10,000 images in the same format for testing the network. This is a typical pattern in machine learning, test and validate the network with a different set of data to prevent overfitting.
The main programming language of machine learning is Python, and so all the examples in Tariq's book are written in this language. But the examples in the book don't depend on a machine learning framework, and so it is quite easy to implement them in another language. For playing with the algorithms, I wrote a Java and JavaScript implementation. There are many matrix calculations involved, so I had to add external libraries to the projects because neither Java nor JavaScript has built-in support for matrices.
Here an overview of the neural network I'm using in the following example.
The network consists of three layers: input, hidden, and output layer. The input layer contains 784 nodes. One node represents one pixel of the scanned image (28 x 28 = 784)
The hidden layer contains 200 nodes, and the output layer 10 nodes.
The purpose of this neural network is to detect the digit that the scanned image contains; therefore it uses 10 output nodes.
For instance if we feed the image of the digit 1 to the network we want as output [0, 1, 0, 0, 0, 0, 0, 0, 0, 0].
Each node between the input and hidden and between the hidden and output layer are connected. To each connection, a weight is assigned. The weight is what changes over time during the learning process.
During the learning process, each image runs through the following steps.
Forward propagation
- Each pixel of the image is assigned to an input node
- For each connection between the input and hidden layer, multiply the value of the input node with the weight and apply an activation function (this example utilizes sigmoid). This value is the result of the hidden layer.
- Do the same for each connection between the hidden and output layer. Multiply the value of the hidden node with the weight and apply the activation function.
Backpropagation
- Compare the values in the output layer with the target values. For instance if we feed the scanned image of a 7 we want
[0, 0, 0, 0, 0, 0, 0, 1, 0, 0]as the output. - To "learn", the network calculates how "wrong" the calculated values are and then adjusts the weight accordingly. The weight adjustment occurs on all layers, output->hidden and hidden-> input.
After step 5, the application feeds the next image into the network and starts over with step 1. It does that for each of the 60,000 images, and it runs the whole process 10 times (epochs).
This is the way how a neural network learns; somebody feeds data into it, compares the output results with the expected results, and tries to minimize the difference by adjusting the weights between the nodes.
In this article I will not go into more detail how all the algorithms work, Tariq does a great job in his book, and my limited machine learning and mathematical knowledge would not suffice to explain this to somebody.
There is also a lot of free information available on the World Wide Web. One blog post I recommend, especially for this example, is https://stevenmiller888.github.io/mind-how-to-build-a-neural-network/, which describes precisely the calculations we use in this neural network.
Example ¶
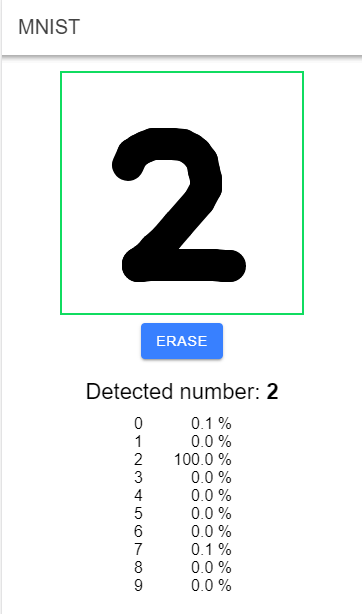
The following example consists of two applications. A Java application for the training process and a JavaScript browser application (Ionic / Angular) for using the pre-trained model to detect digits the user draws into a canvas. The detection process does not depend on any back end server and runs entirely in the browser.
You find the complete source code on GitHub:
https://github.com/ralscha/blog/tree/master/mnist
You can play with the JavaScript application here:
https://omed.hplar.ch/mnist/
Java ¶
The Java application reads the MNIST dataset and trains the network.
The MNIST dataset can be freely downloaded from this website:
http://yann.lecun.com/exdb/mnist/
The application requires all 4 files to be present in the project root directory.
- train-images-idx3-ubyte.gz
- train-labels-idx1-ubyte.gz
- t10k-images-idx3-ubyte.gz
- t10k-labels-idx1-ubyte.gz
The train files contain the training dataset (60,000 images), and the t10k file the 10,000 images of the test dataset.
The images files contain the pixel data of the images, and the label files contain the label for each image. A label is a number between 0 and 9 in string form and corresponds to the scanned image in the images file.
As mentioned before, a lot of the calculations can be quite efficiently handled with matrix calculations. Java does not have built-in support for matrices; therefore, I added the Apache commons-math library to the project.
<dependency>
<groupId>org.apache.commons</groupId>
<artifactId>commons-math3</artifactId>
<version>3.6.1</version>
</dependency>
The application first creates the matrices for the connection between input and hidden and hidden and output layer and then assigns a random weight to each of the connections.
wInputHidden = createRealMatrix(hnodes, inodes);
wHiddenOutput = createRealMatrix(onodes, hnodes);
wInputHidden = initRandom(wInputHidden, Math.pow(inodes, -0.5));
wHiddenOutput = initRandom(wHiddenOutput, Math.pow(hnodes, -0.5));
Next, the application reads the labels and image data from the MNIST files. For each image, it creates two additional images. One rotated 10 degrees clockwise and 10 degrees anticlockwise. This was one of the suggestions in Tariq's book to improve the accuracy of the model.
int[] labels = MnistReader.getLabels(Paths.get("./train-labels-idx1-ubyte.gz"));
List<int[][]> images = MnistReader
.getImages(Paths.get("./train-images-idx3-ubyte.gz"));
double[][] scaledImages = new double[images.size()][];
for (int i = 0; i < images.size(); i++) {
scaledImages[i] = scale(Util.flat(images.get(i)));
}
double[][] roated1ScaledImages = new double[images.size()][];
for (int i = 0; i < images.size(); i++) {
roated1ScaledImages[i] = scale(Util.flat(rotate(images.get(i), 10)));
}
double[][] roated2scaledImages = new double[images.size()][];
for (int i = 0; i < images.size(); i++) {
roated2scaledImages[i] = scale(Util.flat(rotate(images.get(i), -10)));
}
And then, it feeds the three images into the neural network. The application multiplies the input values with the weights and applies the sigmoid function and does the same again from the hidden to the output layer.
// forward
RealMatrix hiddenInputs = wInputHidden.multiply(inputs);
RealMatrix hiddenOutputs = scalar(hiddenInputs, Util::sigmoid);
RealMatrix finalInputs = wHiddenOutput.multiply(hiddenOutputs);
RealMatrix finalOutputs = scalar(finalInputs, Util::sigmoid);
During backpropagation, the application calculates the error between the calculated values and the desired target values and applies a correction value to the weights between output->hidden and hidden->input layer.
// back
RealMatrix outputErrors = targets.subtract(finalOutputs);
RealMatrix t1 = multiplyElements(outputErrors, finalOutputs);
RealMatrix t2 = multiplyElements(t1, scalar(finalOutputs, in -> 1.0 - in));
RealMatrix t3 = t2.multiply(hiddenOutputs.transpose());
wHiddenOutput = wHiddenOutput.add(scalar(t3, in -> learning_rate * in));
RealMatrix hiddenErrors = wHiddenOutput.transpose().multiply(outputErrors);
t1 = multiplyElements(hiddenErrors, hiddenOutputs);
t2 = multiplyElements(t1, scalar(hiddenOutputs, in -> 1.0 - in));
t3 = t2.multiply(inputs.transpose());
wInputHidden = wInputHidden.add(scalar(t3, in -> learning_rate * in));
After running all scanned images through the learning process, the application writes the weights into two files
writeJson(wInputHidden, "./weights-input-hidden.json");
writeJson(wHiddenOutput, "./weights-hidden-output.json");
This is what makes up the "knowledge" of our neural network, the weights between the different layers. We don't need to store the topology of the network, because in this trivial example it is hardcoded (784 input, 200 hidden and 10 output nodes)
The JavaScript application is going to read these two files and utilizes the pre-trained model for detecting user-generated input.
After the learning phase, the program runs the 10,000 test images through the network and calculates an accuracy. In my tests, I got an accuracy of about 97,6 %. Not bad for such a trivial neural network implementation.
JavaScript ¶
The web application is written in TypeScript and uses the frameworks Ionic and Angular. It's a simple application that only consists of one page that displays a canvas element. The user draws a digit with his finger or the mouse on the canvas and the application tries to detect what the digit is, using the pretrained neural network.
Like in Java, JavaScript does not have built-in support for matrix calculations; hence I added the mathjs library to the project.
npm install mathjs
I copied the two weight files from the Java application into the assets folder, so they are part of the application, and I can simply load them with a GET request.
private weightsInputHidden!: number[][];
private weightsHiddenOutput!: number[][];
constructor() {
const fetchInputHidden = fetch('assets/weights-input-hidden.json');
const fetchHiddenOutput = fetch('assets/weights-hidden-output.json');
fetchInputHidden.then(response => response.json()).then(json => {
this.weightsInputHidden = json;
});
fetchHiddenOutput.then(response => response.json()).then(json => {
this.weightsHiddenOutput = json;
});
}
Because the application utilizes a pre-trained model, I only had to implement the forward propagation algorithm. This code works exactly like the Java pendant. Multiply the input value with the weight, and apply the sigmoid activation function, repeat for hidden to output connections.
private forwardPropagation(imageData: number[]): number[] {
const inputs: number[][] = [];
for (const id of imageData) {
inputs.push([id]);
}
const hiddenInputs = multiply(this.weightsInputHidden, inputs);
const hiddenOutputs = hiddenInputs.map(value => this.sigmoid(value));
const finalInputs = multiply(this.weightsHiddenOutput, hiddenOutputs);
return finalInputs.map(value => this.sigmoid(value));
}
Each time the user finished drawing a digit, the application scales down the image to 28x28 pixels.
The user-generated input must be transformed to the same form as the images we used for training.
Then it feeds the 784 pixel values into the forwardPropagation() method and gets back an array with 10 entries. The application chooses the one with the highest score and displays that as the result of the detection process.
Writing your own neural network from scratch is great for learning purposes, but for serious work, you usually use a machine learning framework. Python is the primary language when it comes to machine learning. A lot of courses, examples, and tutorials use this language for explaining machine learning concepts, and many libraries are written in this language.
But there are libraries available for other programming languages. If you are interested in doing machine learning on the Java platform, check out deeplearning4j.
For the JavaScript world check out Tensorflow.js and brain.js.
Many machine learning courses are available online. Here a few free courses that I've found:
- Machine Learning crash course from Google
- Machine Learning with AWS from Amazon
- Practical Deep Learning for Coders from fast.ai
- Cutting Edge Deep Learning for Coders from fast.ai